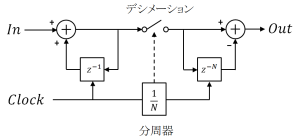
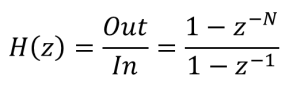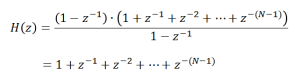ΔΣ型のAD変換器中に図1のようなsincフィルタが使われています。
図1の微分演算は、ClockのN回に1回だけ行われます。デシメーションの記述のあるスイッチは、微分演算の行われる時だけONします。ハードウエアで実現する場合は、スイッチの代わりにD-FFを使っても良いでしょうね。D-FFを使うと、若干の時間遅れが発生すると思いますが、動作確認は容易になります。
伝達関数は、(1)式になりますが、ネットでも簡単に見つかります。
さて、(1)式に下の公式(2)式を適用します。
(2)式において、a=1, n=N, ![]() を代入して、(1)式に適用すると(3)式を得ます。(3)式を分周数Nで割ると、前回投稿した移動平均の式になることがわかります。
を代入して、(1)式に適用すると(3)式を得ます。(3)式を分周数Nで割ると、前回投稿した移動平均の式になることがわかります。
分周数Nとして、2、4、8、……のような2のべき乗を使うと分周器の構成が簡易になり、さらにNで割る操作がデータを構成するビットの右シフトでできるので、良く利用されています。
前回の移動平均のところでも説明しましたが、移動平均のフィルタとしての特性はそれほど優れている訳ではありませんが、図1に示すようにこれ以上簡易な方法は無いほど簡単な回路なので、良く使われています。そして、フィルタ特性の不十分なところは、多段(sinc2, sinc3…)にすることで対応しています。多段の構成については、ネットで簡単に見つけることができるので、そちらを参照ください。
ご意見やご質問がありましたら、遠慮なくご連絡ください。また、間違いや私の勘違いを見つけたら、遠慮なくご指摘ください。
本稿が、ΔΣ型のAD変換器のデータシートの理解に少しでもお役に立てば幸いです。
追記:よく考えてみたら、この場合の移動平均は間引きとセットになっており、どちらかというと間引きがメインで、そのために必要なLPF(Low Pass Filter)を一番簡易に実現できる方式として、このsincフィルタが使われているように思います。この意味で、ΔΣ型のAD変換器とsincフィルタの相性は抜群だと思います。